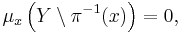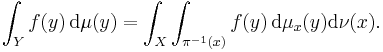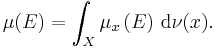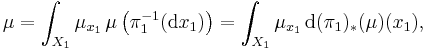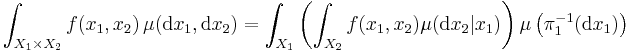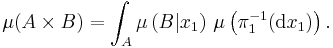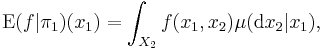Disintegration theorem
In mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures. In a sense, "disintegration" is the opposite process to the construction of a product measure.
Contents |
Motivation
Consider the unit square in the Euclidean plane R², S = [0, 1] × [0, 1]. Consider the probability measure μ defined on S by the restriction of two-dimensional Lebesgue measure λ² to S. That is, the probability of an event E ⊆ S is simply the area of E. We assume E is a measurable subset of S.
Consider a one-dimensional subset of S such as the line segment Lx = {x} × [0, 1]. Lx has μ-measure zero; every subset of Lx is a μ-null set; since the Lebesgue measure space is a complete measure space,
While true, this is somewhat unsatisfying. It would be nice to say that μ "restricted to" Lx is the one-dimensional Lebesgue measure λ1, rather than the zero measure. The probability of a "two-dimensional" event E could then be obtained as an integral of the one-dimensional probabilities of the vertical "slices" E ∩ Lx: more formally, if μx denotes one-dimensional Lebesgue measure on Lx, then
for any "nice" E ⊆ S. The disintegration theorem makes this argument rigorous in the context of measures on metric spaces.
Statement of the theorem
(Hereafter, P(X) will denote the collection of Borel probability measures on a metric space (X, d).)
Let Y and X be two Radon spaces (i.e. separable metric spaces on which every probability measure is a Radon measure). Let μ ∈ P(Y), let π : Y → X be a Borel-measurable function, and let ν ∈ P(X) be the pushforward measure ν = π∗(μ) = μ ∘ π−1. Then there exists a ν-almost everywhere uniquely determined family of probability measures {μx}x∈X ⊆ P(Y) such that
- the function
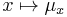 is Borel measurable, in the sense that
is Borel measurable, in the sense that 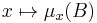 is a Borel-measurable function for each Borel-measurable set B ⊆ Y;
is a Borel-measurable function for each Borel-measurable set B ⊆ Y; - μx "lives on" the fiber π−1(x): for ν-almost all x ∈ X,
- and so μx(E) = μx(E ∩ π−1(x));
- for every Borel-measurable function f : Y → [0, +∞],
- In particular, for any event E ⊆ Y, taking f to be the indicator function of E,
Applications
Product spaces
The original example was a special case of the problem of product spaces, to which the disintegration theorem applies.
When Y is written as a Cartesian product Y = X1 × X2 and πi : Y → Xi is the natural projection, then each fibre π1−1(x1) can be canonically identified with X2 and there exists a Borel family of probability measures 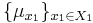 in P(X2) (which is (π1)∗(μ)-almost everywhere uniquely determined) such that
in P(X2) (which is (π1)∗(μ)-almost everywhere uniquely determined) such that
which is in particular
and
The relation to conditional expectation is given by the identities
Vector calculus
The disintegration theorem can also be seen as justifying the use of a "restricted" measure in vector calculus. For instance, in Stokes' theorem as applied to a vector field flowing through a compact surface Σ ⊂ R³, it is implicit that the "correct" measure on Σ is the disintegration of three-dimensional Lebesgue measure λ³ on Σ, and that the disintegration of this measure on ∂Σ is the same as the disintegration of λ³ on ∂Σ. [2]
Conditional distributions
The disintegration theorem can be applied to give a rigorous treatment of conditioning probability distributions in statistics, while avoiding purely abstract formulations of conditional probability. [3]
See also
References
- ^ Dellacherie, C. & Meyer, P.-A. (1978). Probabilities and potential. North-Holland Mathematics Studies, North-Holland Publishing Co., Amsterdam.
- ^ Ambrosio, L., Gigli, N. & Savaré, G. (2005). Gradient Flows in Metric Spaces and in the Space of Probability Measures. ETH Zürich, Birkhäuser Verlag, Basel. ISBN 3-7643-2428-7.
- ^ Chang, J.T.; Pollard, D. (1997). "Conditioning as disintegration". STATISTICA NEERLANDICA 51 (3). http://www.stat.yale.edu/~jtc5/papers/ConditioningAsDisintegration.pdf.
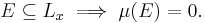
![\mu (E) = \int_{[0, 1]} \mu_{x} (E \cap L_{x}) \, \mathrm{d} x](/2012-wikipedia_en_all_nopic_01_2012/I/3b179f4769a315891a586f0777cab096.png)